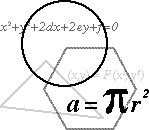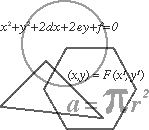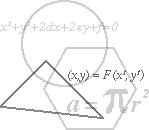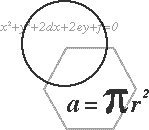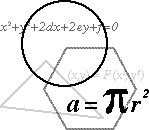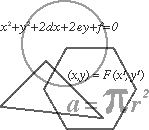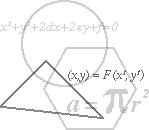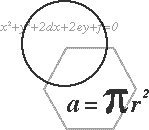1. Проведемо в млинці три прямі і розглянемо точки їх перетину. Залежно від того, де будуть розташовані ці точки, вийде та або інша кількість частин. Щоб отримати 4 частини, треба всі три точки розташувати поза млинцем (мал. 1). Перенесення однієї з цих точок всередину млинця додає одну частину. Так, щоб отримати 5 частин, треба одну точку перенести всередину млинця (мал. 2), 6 — ще одну точку перенести всередину млинця (мал. 3), 7 — всі три точки перетину розмістити всередині млинця (мал.4) 
2. Якщо з трьох прямих кожні дві перетинаються усередині млинця, вийде 7 шматків (мал.4). Якщо ж з цих прямих які-небудь дві паралельні або перетинаються за межами млинця, то шматків буде менше.
3. Для того, щоб піднятися на 2-й поверх, треба пройти 1-й поверх, а для того, щоб піднятися на четвертий — треба пройти три поверхи. Отже, відповідь: у 3 рази (а зовсім не в 2, як здається спочатку).
4. До числа Петі входитимуть цифри 1, 3, 5, 7, 9. Для того, щоб воно було найбільшим, треба цифри в ньому записати строго в зворотному порядку: 97531. У Кольчине ж число увійдуть п'ять цифр 9, і його число буде 99999.
5. Спробуємо поступити, як Чук, — повісимо на кожну гілку по одній іграшці, тоді одна іграшка залишиться зайвою. Тепер візьмемо дві іграшки — одну, що залишилася зайвою, а іншу знімемо з однієї з гілок. Якщо тепер ці іграшки повісити другими на ті гілки, на яких залишилися іграшки від першого разу, тоді на двох гілках висітимуть іграшки і одна гілка залишиться порожньою. Якби, окрім цих трьох гілок, були б ще гілки, то на цих «зайвих» гілках висіло б по одній іграшці, що заперечує умові. Таким чином, гілок було 3, а іграшок, відповідно, 4.
6. З умови виходить, що батько старше за сина на 24 роки. Якщо зараз синові x років, то батьку — 24 +x. Можна скласти рівняння 3x =24 +x. Розв’язавши його, отримаємо x =12. Отже, синові зараз 12 років, а батьку — 36.
7. Спочатку розв’язується завдання а), і з нього вже виводиться розв’язання задачі б). Розв’язання задачі а) приведено в рядках 1–4 таблиці, а розв’язання задачі б) наведено в рядках 1–8 таблиці.

8. Розковуємо 3 кільця з однієї ланки. Що залишилися 4 ланки сполучаємо трьома розкутими кільцями.
9. Позначимо шукане число через x і запишемо рівняння: 4x +15 =15x +4. Розв’язуючи це рівняння, отримаємо: 11 =11x, або x =1.
10. Перша пані за свою покупку заплатила як за 13 маленьких птиць (нагадаємо, що велика птиця в два рази дорожче маленької), а друга — як за 11 маленьких. Тобто різниця в покупках — 2 маленькі птиці, а різниця в ціні — 20 грн. Означає, маленька птиця коштує 10 грн., а велика — 20 грн.
11. Для зручності повторимо всі умови завдання: 1) червона фігура — між синьою і зеленою; 2) праворуч від жовтої фігури — ромб; 3) круг — правіше і трикутника і ромба; 4) трикутник — не з краю; 5) синя і жовта фігури — не поруч. Оскільки червона фігура лежить між синьою і зеленою (умова 1), а жовта — не поряд з синьою (умова 5), то можливі лише два варіанти розташування фігур за кольором: «синя, червона, зелена, жовта» або «жовта, зелена, червона, синя». Перший з приведених варіантів неправильний, оскільки (за умовою 2) жовта фігура не може лежати на правому краю. Залишається лише одна можливість розташування фігур за кольорами: «жовта, зелена, червона, синя». З умови 2 відразу ж визначається, що ромб зелений. Звідси і з умови 4 витікає, що трикутник червоний. У свою чергу звідси і з умови 3 витікає, що круг синій. Значить, прямокутник може бути лише жовтим. Остаточна відповідь: жовтий прямокутник, зелений ромб, червоний трикутник, синій квадрат.
12. Продавець дав покупцеві товару і здачі на суму 100 грн., та ще другому продавцеві заплатив 100 грн., але і від другого продавця він заздалегідь отримав 100 грн. Отже вся пропажа — 100 грн. Можна розв’язати і по-іншому. Покупець, фактично, «недодав» продавцеві 100 грн. На цих-то 100 грн. і погорів продавець.
|